(C) 2004 Hank Wallace
For the geeks in the crowd, what follows is a technical description of what RMS means and how to compute it. If you are not technically inclined, then be warned that you may require counseling to return to normalcy, if you read further. Those who slept through less than 50% of high school algebra should be able to follow. [There is a note at the end of this discussion for engineers.]
Power is computed by multiplying the current flowing in the speaker cable by the voltage measured between the two wires in the speaker cable. Measuring the power flowing from your amplifier to speaker can be done in several ways, but each way is a variation on this theme.
Think of the current like water flowing in a pipe, and the voltage being like the water pressure. More pressure produces more water flow, just like more voltage produces more current flow.
The impedance of the speaker is like a turbine in the water pipe, where the water does some work, like turning a generator and making electricity in a hydroelectric dam. The lower the impedance, the bigger the turbine and the greater the power extracted from the flow of water. A lower impedance speaker extracts more power from the flow of electricity from the amplifier, and makes more sound (within limits).
For a steady voltage driving a steady load, like a battery driving a light bulb, it is easy to compute the power. In a flashlight we have three volts (two 1.5V batteries). If there are 2 amps flowing to the light bulb, then the power is 3 volts times 2 amps = 6 watts.
There’s a simple law of electronics called Ohm’s law that tells us the impedance of the light bulb is the voltage divided by the current, or 3 volts / 2 amps = 1.5 ohms. (Impedance is measured in units called ohms, just like you are familiar with for speakers.)
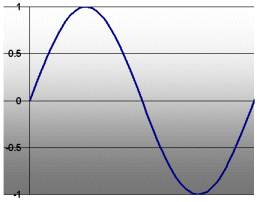
It’s more complicated with audio signals because they change continuously. Here’s a voltage graph of the note as might be heard from a bell or chime, called a sine wave, as pictured.
Now the question is, how big does the sine wave have to be to get 6 watts of power into that light bulb? (The size of the sine wave pictured is 1 volt, as you can see in the top left corner.)
If the top of the sine wave has a value of 3 volts (called a peak value), you might suspect the power will be considerable but less than 6 watts. Intuitively, it looks like the “value” of the waveform in some sense is less than 3 volts from the batteries.
That’s right. So, what peak value of the voltage do we need to get 3 volts as the effective value of the waveform, producing 6 watts in the light bulb?
This is where RMS comes in to play. Skipping the potentially brain damaging math, it turns out that the RMS (also called “effective value”) of a sine wave is 0.707 times the peak value. (1/0.707 is the square root of two; that is, 1/0.707 times 1/0.707 equals 2.)
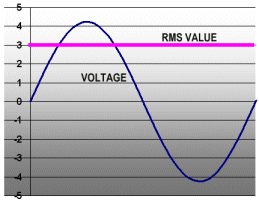
So, to pump 6 watts into that light bulb, we need a sine wave with a peak value of 3 volts divided by 0.707, or 4.24 volts. Not exactly something you would have guessed, right? The graph shows the sine wave and its effective or RMS value (the purple line at 3 volts). The sine wave and the steady voltage at 3 volts both produce the same power in the light bulb.
Let’s look at the electric current flowing in the light bulb, too. The current is 2 amps (see above), but that’s only the RMS value. The current is a sine wave, too. What is the peak value of the current? It is simply 2 amps divided by 0.707, or 2.83 amps. See yellow curve in the graph.
Now we have a way to determine the power flowing into the light bulb for audio signals, at least sine waves made by pure tones like chimes and guitar harmonics. First, we find the peak values of the voltage and current sine waves. Next we multiply them each by 0.707. Finally, we multiply those two numbers together to get the power. This table shows the power for several voltages and currents.
| Voltage | Current | Power |
|---|---|---|
| 1 volt | 0.67 amps | 0.67 watts |
| 2 volts | 1.33 amps | 2.67 watts |
| 3 volts | 2.00 amps | 6.00 watts |
| 4 volts | 2.67 amps | 10.67 watts |
| 5 volts | 3.33 amps | 16.67 watts |
| 6 volts | 4.00 amps | 24.00 watts |
| 7 volts | 4.67 amps | 32.67 watts |
| 8 volts | 5.33 amps | 42.67 watts |
| 9 volts | 6.00 amps | 54.00 watts |
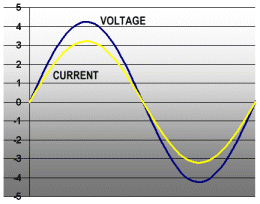
Ahh, but there’s a catch. The methods above work great for flashlight bulbs, but not speakers! See, there is an incomprehensible effect that occurs when you wind a wire around a hunk of steel, like in the voice coil of a loudspeaker. That effect is called inductance, and it is an interaction of the magnetic field (caused by the speaker current) and the current itself. Without doing any more brain damage, the basic result is that the current and voltage sine waves do not line up in time. See the graph below.
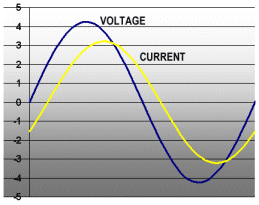
For inductive speakers, the voltage always starts increasing before the current. How do we compute the power being delivered to the speaker now that the waveforms do not line up? It would seem that all we need to do is figure the RMS voltage and RMS current (using our friend 0.707), and multiply them together. Unfortunately, that’s not the case.
For sine waves, we can come up with a mathematical shortcut to find the power which is related to the amount of offset between the voltage and current. But for real signals, like music, that won’t work because the signals are too complicated.
Here’s where the twist comes in the story. What we do is consider the voltage and current waveforms point by point. The power at any instant in time is the voltage times the current at that instant.
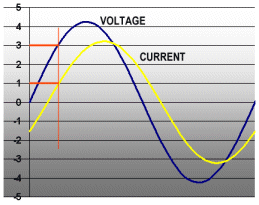
The power at the point marked by the vertical red line is 3 volts times 1 amps, or 3 watts. But the power is changing continuously! What do we do?
Engineers have figured out that the power in a waveform such as this is computed in the following way:
- Figure the instantaneous power (voltage times current) at a bunch of regularly spaced points. This would be hundreds or thousands of points typically.
- Add up all the instantaneous powers.
- Divide the sum by the time period the points came from.
The result is the true power! This method works on any kind of waveform, for any impedance speaker, with any amount of inductance. The next time you see the term “RMS” you’ll have a little respect!
Needless to say, figuring the value of the power flowing to your speaker is a computationally intensive task. That’s one of the things that makes the PM-150 power meter so special. It does all these computations for you in real time, all without you suffering any mathematically induced brain damage.
The conclusion is that the power represents the amount of heat and light that would be generated in a light bulb with the set voltages and currents. This is also directly related to how much sound the speaker is making. That’s what the PM-150 was designed to measure.
Why do we use the term TRUE RMS? Because there’s such a thing as calibrated RMS measurement. It’s really a throwback to the good old days where true RMS measurements costs thousands of dollars. Engineers used cheaper meters that responded to the average signal level, then changed the markings on the meter faces to read RMS. This works OK for sine waves, but is terrible for music because it has such an unpredictable waveform with so many peaks. However, there are calibrated RMS power meters on the market even today, so be sure that you are using a PM-150 which displays the proper power, regardless the type of audio.
[For the engineer: You have read that there is no such thing as “RMS power.” Technically, you are right. However, over the years the term, regarding audio gear, has come to be applied to the measurement technique outlined above, so we use that language here, rather than terminology with which the customer is unfamiliar. Yes, the computation is mathematically an integral of the instantaneous power.]
