(C) 2010 Hank Wallace
Certainly you have experimented with the order of pedals on your pedal board. You have noticed that the order of connection of the pedals affects the sound. Most articles that mention pedal order tell you what the ‘best’ order is. Some articles explore what ordering famous guitarists use. What I am going to cover here is exactly why pedal order makes a difference in the sound. You can decide for yourself what is best!
What we suspect is that chorusing a distorted signal is not the same as distorting a chorused signal. This situation actually appears commonly in language, engineering and mathematics, and is easy to understand in those terms.
For example, let’s start with a couple simple phrases:
- Bill got drunk.
- Bill played guitar with his band.
The order of these phrases is important, as anyone who has played in a band with a heavy drinker will understand! Keeping Bill away from the beer before the gig ensures a good night. But if Bill gets loaded before the gig, well, let’s just say you won’t be invited back! The order of the actions produces entirely different results.
In math, you can add numbers in any order (5+1 equals 1+5), but you cannot subtract numbers in any order (5-1 is not equal to 1-5). This shows you that order is important. You certainly remember your 5th grade math teacher, Mrs. Gelbottom, and her bee hive hairdo, caked on makeup and obnoxious perfume. Remember how she harped on the Commutative Property of Addition and Multiplication, and how subtraction was not commutative?
In the discipline of signal processing, order of operations is critical. And signal processing is just what we are doing with guitar effects pedals, no matter how cheap or simple they are! It turns out that some effects are not commutative, and some are.
In signal processing, engineers typically use block diagrams to illustrate how their systems are constructed. Engineers understand which blocks can be swapped, and which must be in a certain order. If the blocks are swapped out of order, your cell phone quits working!
Think of your pedals as some of those signal processing blocks. As a guitarist, you can do whatever swapping you want with your pedals and your amp will still produce ear bleed tones, but perhaps not the sounds you expect.
For example, take flanging and distortion. Flanging is a frequency-domain effect that changes the signal’s basic frequencies, sweeping them back and forth, while mixing in some of the dry signal. Distortion takes the relatively simple waveform from your guitar and clips it, resulting in a much more complex spectrum.
Let’s look at some signals, and you will be able to see clearly what the order of the pedals does. I took a simple tone and crunched it through some effects in a DAW software package.
And here is what it looks like.
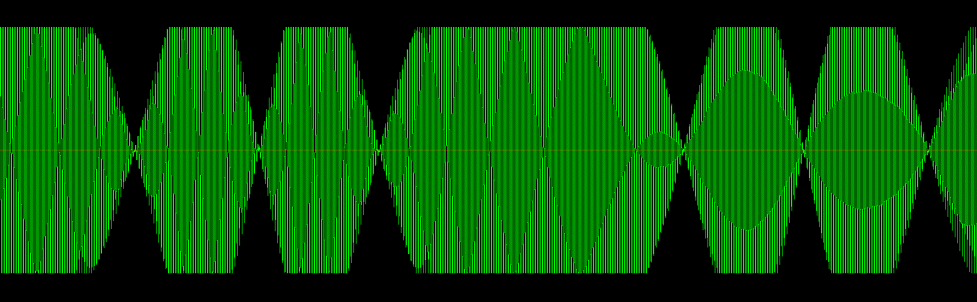
I first processed the waveform with a flanger effect which had a 50/50 wet/dry mix, then clipped it. Here is the look of the resulting waveform (click to enlarge):
Listen to the flanged-then-clipped waveform:
The flanger effect with the 50/50 mix causes the waveform nulls as the dry and wet signals cancel periodically. You can hear these nulls clearly as the wave plays. You can hear the clipping when the full volume sections are playing (that fatter, square wave sound), and you can hear the lower volume sections are not so fat sounding because they are not clipped.
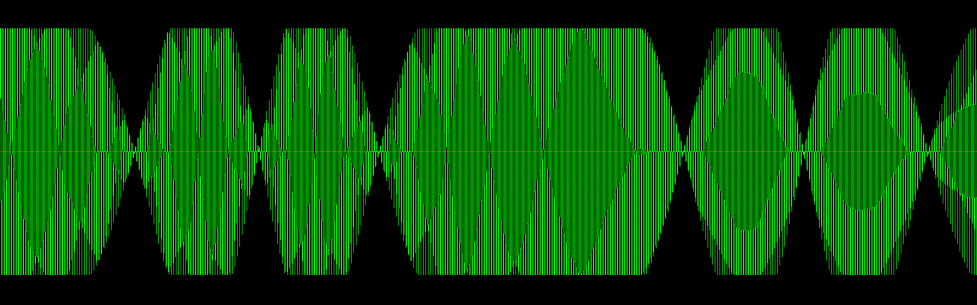
As a second test, I clipped the original tone waveform, and processed it with the same flanger effect settings. Here is the look of the resulting waveform:
The flanger effect with the 50/50 mix causes the waveform nulls as before, but the sound of the wave is entirely different. This is because every cycle of the waveform was clipped and has a smeared audio spectrum as a result (the fat sound). Flanging that waveform results in nulls, but since the harmonic content of the waveform was so much greater to begin with, the nulls are not so noticeable.
If you put the flanger (or chorus) before a distortion pedal, as in the first example, you will end up with a simpler sound. If you put the distortion pedal first, the flanger (or chorus) effect will take that complex spectrum and make it even more complex. Depending on the song you are playing, you can select the pedal order to get the sound you desire.
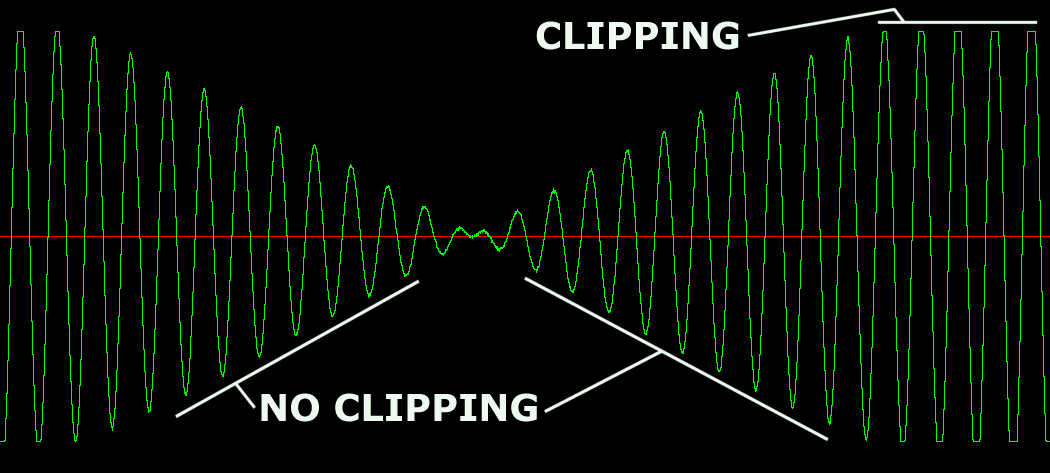
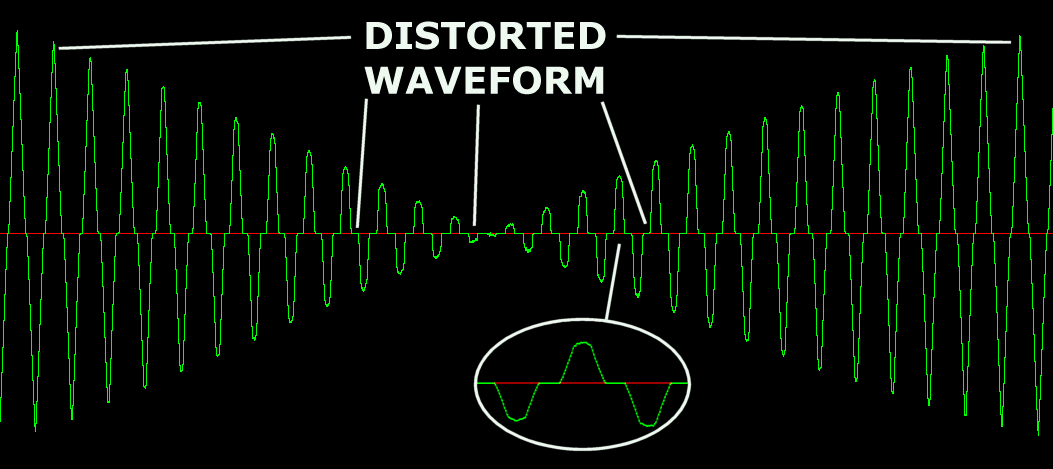
Let’s look at the waveforms under a magnifying glass. The flange-then-clip waveform looks like this:
You can see that the original flanged signal is preserved below the clipping level. The signal here is a simple tone, fading in and out, and changing frequency, and you can hear that in the sound clip.
The clip-then-flange waveform looks like this:
You can see here that the flanged signal has some of the character of the clipped signal, that is, distortion. The zero crossings are not continuous, and the waveform peaks are not smooth. This signal has a much broader spectrum through the null dips.
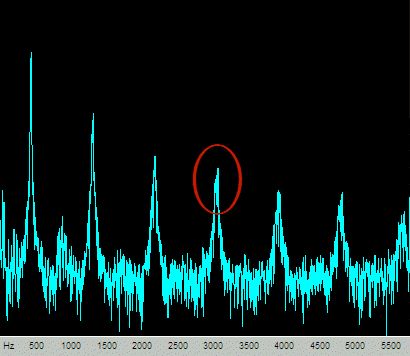
Let’s look at the spectrums of the waveforms. The flange-then-clip waveform looks like this:
This waveform has a smearing of the harmonics of the clipped signal. I’ve circled the seventh harmonic (7 * 440Hz = 3080Hz). These harmonics are due to the symmetric clipping, which produces odd harmonics only. The even harmonics are very low level and are between the large peaks. The flanging effect sweeps the tone back and forth around its 440Hz value, and the harmonics sweep as well, but the sweep is easier to see in the harmonics because the deviation is multiplied by seven.
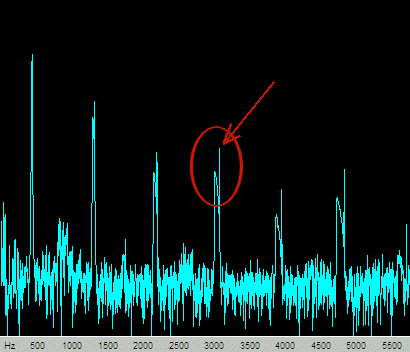
Here’s the spectrum of the clip-then-flange waveform:
This one looks similar, except there is a sharp peak with every harmonic (see the arrow), and this accounts for the fat sound, even through the nulls (where this spectrum was sampled). These peaks are due to the 50% dry mix implemented in the flanger, the dry signal being clipped.
This non-commutative property of audio effects complicates things, but it also gives you a multitude of tonal possibilities. Guitarists are always trolling auction sites and flea markets for effects pedals, searching for that sound, when they actually have a huge bag of sounds in the few pedals they own. Just rearranging the pedals on your pedalboard can open up new vistas of tone.
Here are some things to try:
- Swap the order of your distortion and compressor pedals. Compressor before distortion gets you closer to the infinite sustain that some players covet. Distortion before compressor can preserve some of the dynamics you love about your distortion pedal.
- Swap the order of your distortion and modulation pedals (chorus and flanger). Distortion before modulation gives the chorus or flanger pedal a more complex spectrum to work with.
- Swap the order of your distortion and delay pedals. Distortion before delay ensures that all the echo tails will be distorted. Delay before distortion can leave the echo tails clean as they decay.
- Some effects widen the spectrum of your signal, distortion for example, and modulation effects to a lesser extent. If you use wilder effects like a ring modulator or pitch shifter, adding these spectrum widening effects before them in the chain can produce some dramatic sounds.
Be sure you try the various sounds with your band wailing, as the perceived sound at a gig will be totally different from the perceived sound in your bedroom!
Some effects are actually commutative. For example, chorus and tremolo. The chorus effect operates in the frequency domain, producing frequency modulation (FM), and the tremolo effect operates totally in the amplitude domain, producing amplitude modulation (AM). These two effects are independent of one another, so you can connect chorus and tremolo pedals in either order and get the same sound (at low rates, and as long as the pedals introduce no distortion).
As a matter of fact, there are patents on simultaneous transmission of radio signals using AM and FM, with each modulation carrying different information.
With commonly available pedalboard switching gizmos, you could actually have setups that reorder your pedals on the fly, in the middle of a gig! Use your imagination and do some experiments. Then go find Mrs. Gelbottom on Facebook and tell her that you finally understand the commutative property!